Versija spausdinimui

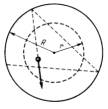
1. Rutuliukas rieda loveliu žemyn nuo aukščiausio taško be pradinio greičio. Lovelis sukasi apie vertikalią ašį kampiniu greičiu ω. Raskite rutuliuko Koriolio pagreičio priklausomybę nuo laiko. Lovelio ilgis l, kampas su vertikale φ. (Pav. 3)

10. Duotos taško koordinačių priklausomybės nuo laiko: x(t)=t-sin(t) ir y=1-cos(t) (t – laikas sekundėmis, x ir y - metrais). Raskite greičio v, pagreičio a, tangentinio pagreičio a_τ, normalinio pagreičio a_n ir jų modulių priklausomybes nuo laiko.

12. Pavargęs pilietis bando pereiti gatvę, kurios plotis d = 8 m. Jo ėjimo trajektorija y(x) = sin(0.5πx) (x ašis statmena šaligatviui), greičio modulis  . Kiek laiko užtruks piliečiui pereiti gatvę?

18. Vertikaliai žemyn greičiu v krentantį stalo teniso kamuoliuką olimpietis smūgiuoja rakete taip, kad iškart po smūgio kamuoliukas juda horizontaliai. Raketės greitis prieš smūgį u. Kokiu kampu φ su vertikale buvo laikoma raketė ir koks kamuoliuko greitis v‘ po smūgio. Smūgį laikykite tampriu.

20. Ant nuožulniosios plokštumos (kampas su horizontu 30^o) žemyn metamas kamuoliukas. Pradinis kamuoliuko greitis v = 1 m/s. Kokiu kampu su horizontu turi būti metamas kamuoliukas, kad atstumas tarp pirmų dviejų taškų, kuriuose jis atšoka nuo plokštumos, būtų didžiausias. Netampraus smūgio į plokštumą metu statmenos plokštumai greičio dedamosios modulis sumažėja per pusę.

                   Pav. 3                          

Užduotis parengė VU Fizikos fakulteto III kurso studentas Donatas Majus, donatas.majus@ff.vu.lt.

Užduočių sprendimus iki 2006 12 15
išsiųskite mokyklos adresu 
Saulėtekio al. 9, III rūmai, 200 kab., 10222 Vilnius, 
ant voko papildomai užrašę „Donatui Majui“
 

Pastaba: pavėluotai išsiųsti užduočių sprendimai netikrinami ir nevertinami.